Using Mixed Methods to Answer
Multidimensional Research Problems

In my UX Portfolio, I explain the different mixed methods approaches that I use to address each type of research question. Below, I provide two examples of how I combined approaches to address multidimensional research problems. Solving for these types of larger foundational issues drives novel solutions for individual decision making, product development, and company innovation.

Academic Research Program: Understanding Diagnostic Test Statistics

Research Problem: In medicine, both patients and medical providers have difficulty understanding and interpreting diagnostic test results and how testing accuracy rates apply to them personally. A single diagnostic test result often includes an overwhelming amount of medical statistics. Yet, people perceive numbers as complicated and potentially irrelevant. Mathematical operations are seen as cumbersome. More often than not, though, people simply do not know how to use these numbers in their health decision making.

Purpose of Research Program: To help doctors and patients understand medical statistics in a way that informs personal medical and health decision making. More importantly, this research was dedicated to helping patients and doctors become informed decision makers within their shared health maintenance and treatment plans.

Approach: I created a research program using mixed methods to address different pieces of the overall problem. Each step was designed to address an individual section of the multidimensional problem, with results incorporated into the subsequent phases of the research. Triangulation of all these data points led to a cohesive solution which was implemented in medical training programs across the US.

Solution: Modify presentation of diagnostic test information to focus specifically on the the patient’s and provider’s information request. Provide additional context using progressive reveal as each piece of information becomes understood and incorporated into the decision making process.

Phase 1: Focus Groups

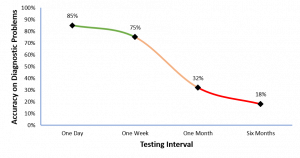
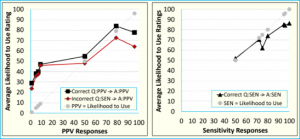
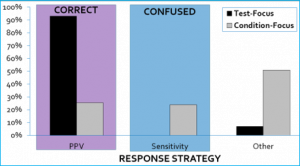
To begin, we ran focus groups to get impressions and assessments of traditional presentation formats for diagnostic accuracy. Calculations for these values are traditionally taught using complicated grids such as the one presented to the right.

Major takeaway: Not only are patients confused by numbers, but doctors are as well! Lo and behold, doctors hate numbers almost as much as my stat 101 students do. These findings informed a set of longitudinal studies to assessed formal learning of predictive values in a classroom setting.

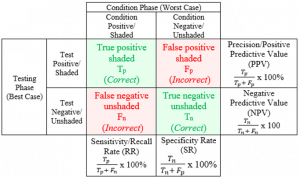
Traditional grid for calculating important diagnostic test result values.

Phase 2: Longitudinal Assessment

The methods I use to teach medical statistics are the same I use to teach null hypothesis testing, the predominant form of statistical analyses used around the world. Students from my stats course agreed to participate in this study for extra credit. Assessment occurred one week after finals (brutal I know), one month later, and then six months later.

Major takeaway: Learning the complex statistical calculations required to work with these kinds of numbers didn’t stick. Learning was relatively good after a week or so, but then dropped dramatically.

As documented in numerous studies across domains, learning retention drops off significantly after consistent exposure to material is removed.

Phase 3: Experimentation and Brief Tutorials

I switched gears at this point and created a short, 5 minute 1:1 self-guided tutorial using different types of visuals to see which would help the most. What I found was that it helped better than my statistics course (which incidentally made me rethink how I teach statistics).

Major takeaway: The training was impactful and to the point, with immediate feedback provided after completion of the tutorial. People easily completed this in under 5 minutes, which could be employed in medical waiting room. Colleagues adopted this to teach future MDs and found that it improved their understanding of medical statistics as well!

Caveat: Additional research suggests that even after developing proficiency, these MDs in training were hesitant to use the new skills in-vitro. Their confidence in their own abilities to properly explain complicated medical statistics overruled any learning they accomplished.

A brief tutorial increased accuracy almost as much as a full semester of learning how to calculate diagnostic statistics.

Likelihood to use the test was highly correlated with the evaluated diagnostic value. Tests with lower diagnostic values are less likely to be used and vice versa.

Phase 4: Theoretical Underpinnings

In the final phase of this research, I used a series of controlled lab experiments. In these studies, I evaluated numeric confidence, or how well someone thinks they are with numbers, and working memory. I hypothesized that both relate to and affect an individual’s ability to understand and use statistics in personal decision making.

I looked at where people were getting answers right, and where they were getting confused. Process tracing and basic eye tracking were used to determine missed opportunities within the computational process. In the end, I discovered the use of statistics within decision making is not as simple as taking a number and applying it.

Major takeaway: I found that simple restructuring of diagnostic information to match the question and response expectations was the most beneficial for increasing understanding of diagnostic testing statistics. The higher the accuracy for identifying different diagnostic values, the more likely patients and medical providers are to utilize this information to inform their medical and health decisions.

Matching the diagnostic information between the question and response needed increased accuracy to over 90% across 8 unique problems. Participants easily identified the correct value and were less likely to confuse related diagnostic values when information matched expectations.

Computation is more than just mathematical manipulation of values, but instead involves many steps to determine the correct response.